Calculando a Área de um Triângulo Equilátero: 7 Mostre Um Exemplo Envolvendo Área De Um Triângulo Equilátero
Mostre Um Exemplo Envolvendo Área De Um Triângulo Equilátero – A área de um triângulo equilátero, figura geométrica de três lados iguais e três ângulos internos de 60 graus, é um conceito fundamental em geometria com aplicações práticas em diversas áreas. Compreender sua fórmula e aplicações é crucial para resolver problemas em contextos que vão da construção civil à engenharia.
Introdução à Área do Triângulo Equilátero
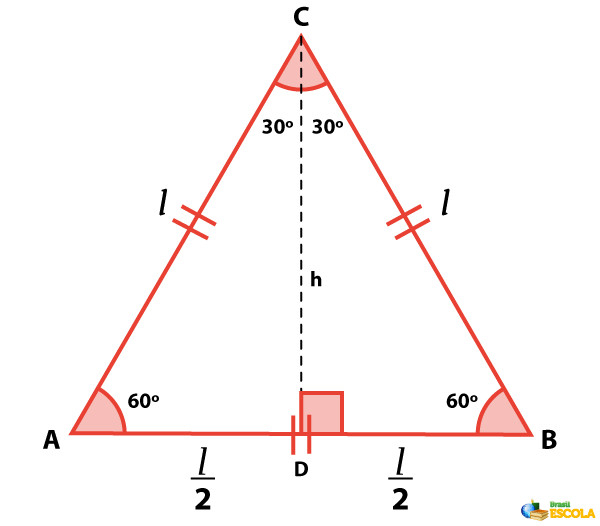
A fórmula para calcular a área (A) de um triângulo equilátero é dada por:
A = (l²√3)/4
onde ‘l’ representa o comprimento de um dos lados do triângulo. A fórmula deriva da aplicação do teorema de Pitágoras em um triângulo retângulo formado ao dividir o triângulo equilátero em dois triângulos retângulos congruentes, utilizando a altura como um dos catetos. A multiplicação por √3/4 resulta da relação entre a altura e o lado do triângulo equilátero, e a multiplicação por 1/2 representa a área de um triângulo qualquer (base x altura / 2).
A diferença crucial entre a fórmula da área do triângulo equilátero e a fórmula geral da área de um triângulo (base x altura / 2) reside na sua simplicidade: a fórmula do triângulo equilátero expressa a área diretamente em função do comprimento do lado, eliminando a necessidade de calcular a altura separadamente. A semelhança, naturalmente, é que ambas calculam a área do triângulo.
| Etapa | Descrição | Cálculo | Resultado |
|---|---|---|---|
| 1 | Definir o comprimento do lado (l) | l = 5 cm | 5 cm |
| 2 | Substituir ‘l’ na fórmula | A = (5²√3)/4 | (25√3)/4 cm² |
| 3 | Calcular o valor aproximado | A ≈ (25 – 1.732)/4 | A ≈ 10.83 cm² |
Exemplos de Cálculo da Área

A aplicação da fórmula é direta. Consideremos três exemplos: um triângulo com lado de 3cm, outro com lado de 10cm, e um último com lado de 7cm. Os cálculos resultariam nas seguintes áreas:
- Triângulo com lado de 3cm: A = (3²√3)/4 ≈ 3.897 cm²
- Triângulo com lado de 10cm: A = (10²√3)/4 ≈ 43.30 cm²
- Triângulo com lado de 7cm: A = (7²√3)/4 ≈ 21.22 cm²
Em um projeto de construção civil, imagine o telhado de uma casa com uma seção triangular equilátera, com cada lado medindo 8 metros. Para calcular a quantidade de telhas necessárias, a área dessa seção é fundamental. Utilizando a fórmula, a área seria A = (8²√3)/4 ≈ 27.71 m².Um cenário onde o conhecimento da área é essencial é a determinação da quantidade de material para cobrir uma superfície triangular em um projeto de paisagismo.
Sabendo a área, o paisagista pode calcular a quantidade de grama ou outros materiais necessários.
Aplicações da Fórmula em Diferentes Contextos

A fórmula da área do triângulo equilátero encontra aplicações em diversas áreas. Em geometria, é fundamental para o cálculo de áreas e perímetros em figuras mais complexas. Em engenharia, pode ser usada para calcular a área de seções transversais em estruturas. Na arquitetura, é útil no planejamento e dimensionamento de estruturas com formas triangulares. A eficiência da fórmula reside na sua simplicidade e precisão, superando métodos aproximados que poderiam levar a erros significativos.
A dedução da fórmula, como mencionado anteriormente, se baseia em conceitos básicos de geometria, utilizando a divisão do triângulo em dois triângulos retângulos e a aplicação do teorema de Pitágoras.
Relação entre Lado e Área
Existe uma relação quadrática entre o comprimento do lado de um triângulo equilátero e sua área. Isso significa que, ao dobrar o comprimento do lado, a área aumenta quatro vezes. Um gráfico mostrando essa relação seria uma parábola, onde o eixo x representa o comprimento do lado e o eixo y representa a área. A construção deste gráfico envolve o cálculo da área para diversos valores de lado e a posterior plotagem dos pontos em um sistema de coordenadas cartesianas.
Claramente, um aumento no comprimento do lado resulta em um aumento significativo na área do triângulo equilátero.
Problemas e Desafios, 7 Mostre Um Exemplo Envolvendo Área De Um Triângulo Equilátero
Um problema desafiador envolve calcular a área de um triângulo equilátero inserido dentro de um hexágono regular. A solução envolve dividir o hexágono em triângulos equiláteros congruentes e calcular a área de cada um. Em situações onde a medição precisa do lado é difícil, uma aproximação da área pode ser necessária, utilizando técnicas de medição indireta e cálculos trigonométricos.
Um problema que envolve uma equação seria: “Um triângulo equilátero tem área de 25√3 cm². Qual o comprimento do seu lado?”. Resolvendo a equação A = (l²√3)/4 para ‘l’, encontramos l = 10 cm.
Dominar o cálculo da área de um triângulo equilátero transcende a mera aplicação de uma fórmula; representa a compreensão de princípios geométricos fundamentais e sua aplicabilidade em situações diversas. De projetos arquitetônicos a desafios de engenharia, a precisão nesse cálculo garante eficiência e otimização de recursos. Esperamos que esta jornada tenha iluminado a importância desta fórmula aparentemente simples, mostrando sua potência e versatilidade em um amplo espectro de aplicações.
Lembre-se: a geometria não é apenas teoria; é uma ferramenta poderosa para solucionar problemas do mundo real, e o triângulo equilátero é um exemplo brilhante disso.

