Conceitue A Estutura De Dados Grafo E Cite Dois Exemplos – Conceitue A Estrutura De Dados Grafo E Cite Dois Exemplos: A estrutura de dados grafo, presente em diversas áreas da computação, representa relações entre entidades. Sua flexibilidade permite modelar sistemas complexos, desde redes sociais até mapas rodoviários. Compreender seus conceitos fundamentais, como vértices, arestas, e tipos de grafos (direcionados e não direcionados), é crucial para a aplicação eficiente em algoritmos de busca, análise de redes e muito mais.
Este estudo explorará a definição de grafos, suas representações (matrizes e listas de adjacência), e apresentará exemplos práticos em redes sociais e mapas rodoviários, ilustrando sua versatilidade e importância na ciência da computação.
Introdução ao Grafo
Os grafos, na ciência da computação, são estruturas de dados que representam relações entre objetos. Imagine um mapa de estradas: as cidades são os objetos, e as estradas que os conectam são as relações. Essa é a essência de um grafo, uma ferramenta poderosa para modelar diversas situações do mundo real.
Grafos Direcionados e Não Direcionados, Conceitue A Estutura De Dados Grafo E Cite Dois Exemplos
A principal diferença entre grafos direcionados e não direcionados reside na natureza das conexões entre os objetos (vértices). Em um grafo não direcionado, a relação é mútua: se o vértice A está conectado ao vértice B, então B também está conectado a A. Já em um grafo direcionado, a relação é unidirecional: a conexão de A para B não implica necessariamente uma conexão de B para A.
Pense em um mapa de ruas de mão única: o tráfego flui apenas em uma direção.
Componentes Básicos de um Grafo: Vértices e Arestas
Os vértices são os objetos que o grafo representa. Eles podem ser cidades em um mapa, pessoas em uma rede social, ou qualquer outro elemento que necessite ser modelado. As arestas são as conexões entre os vértices, representando a relação entre os objetos. Elas podem ser direcionadas (com uma direção específica) ou não direcionadas (bidirecionais).
Tipos de Grafos
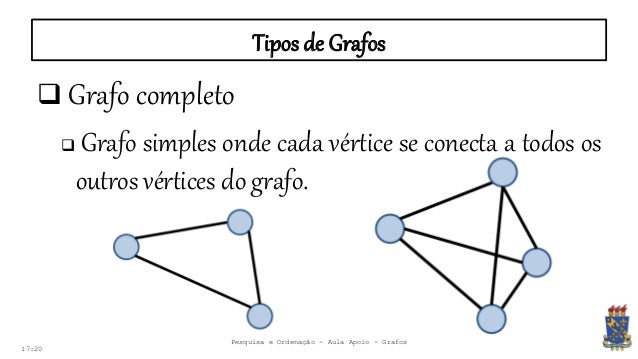
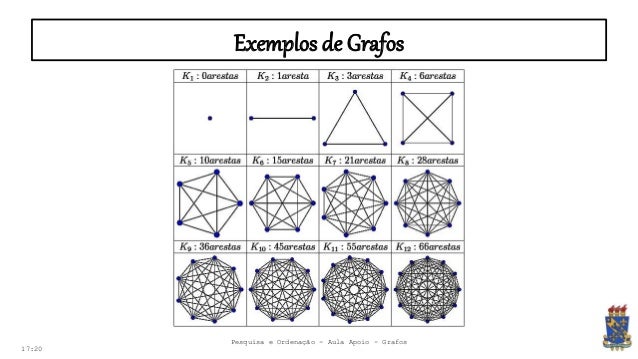
Existem diversos tipos de grafos, cada um com características próprias. Grafos completos, por exemplo, possuem uma aresta conectando cada par de vértices. Grafos cíclicos contêm ciclos (caminhos que começam e terminam no mesmo vértice), enquanto grafos acíclicos não possuem ciclos. Grafos ponderados atribuem pesos às arestas, representando, por exemplo, distâncias ou custos.
Representação de Grafos
Existem duas maneiras principais de representar grafos: matriz de adjacência e lista de adjacência. A escolha da melhor representação depende da aplicação e das características do grafo.
Matriz de Adjacência vs. Lista de Adjacência
Ambas as representações têm suas vantagens e desvantagens. A matriz de adjacência é simples de implementar, mas pode ser ineficiente para grafos esparsos (com poucas arestas). Já a lista de adjacência é mais eficiente para grafos esparsos, mas pode ser mais complexa de implementar.
| Característica | Matriz de Adjacência | Lista de Adjacência |
|---|---|---|
| Espaço de Armazenamento | O(V²) | O(V+E) |
| Verificar Adjacência | O(1) | O(V) |
| Listar Vizinhos | O(V) | O(grau(V)) |
| Eficiência para Grafos Esparsos | Ineficiente | Eficiente |
Representação de um Grafo Simples
Vamos considerar um grafo simples com quatro vértices (A, B, C, D) e as seguintes arestas: A-B, A-C, B-C, C-D.
| Matriz de Adjacência | Lista de Adjacência |
|---|---|
[ [0, 1, 1, 0], [1, 0, 1, 0], [1, 1, 0, 1], [0, 0, 1, 0] ] |
A: [B, C] |
Aplicações de Grafos – Exemplo 1: Redes Sociais
Redes sociais são modeladas naturalmente como grafos. Cada usuário é um vértice, e uma aresta conecta dois usuários se eles são amigos. A análise de grafos permite descobrir comunidades, influências e conexões ocultas.
Modelo de Rede Social como Grafo
Imagine uma pequena rede social com três usuários: Alice, Bob e Carol. Alice é amiga de Bob e Carol, enquanto Bob e Carol não são amigos. Neste caso, Alice, Bob e Carol são os vértices, e as amizades são as arestas não direcionadas. Encontrar conexões envolve percorrer as arestas para determinar o caminho entre usuários, usando algoritmos como busca em largura ou profundidade.
Um diagrama visual mostraria três círculos (Alice, Bob, Carol) com linhas conectando Alice a Bob e Alice a Carol. A ausência de uma linha entre Bob e Carol indica a falta de amizade direta entre eles.
Aplicações de Grafos – Exemplo 2: Mapas Rodoviários: Conceitue A Estutura De Dados Grafo E Cite Dois Exemplos
Mapas rodoviários são outra aplicação clássica de grafos. As cidades são representadas por vértices, e as estradas que as conectam são as arestas. A distância entre as cidades pode ser representada pelo peso das arestas.
Modelo de Mapa Rodoviário como Grafo
Consideremos um mapa simplificado com três cidades: São Paulo, Rio de Janeiro e Belo Horizonte. São Paulo está conectada ao Rio e a Belo Horizonte, enquanto Rio e Belo Horizonte não estão diretamente conectados. Cidades são os vértices, e as rodovias que as ligam são as arestas. Um algoritmo de caminho mais curto, como o algoritmo de Dijkstra, poderia calcular a rota mais eficiente entre duas cidades, considerando a distância (peso) de cada estrada.
O diagrama visual mostraria três círculos (São Paulo, Rio de Janeiro, Belo Horizonte) com linhas conectando São Paulo ao Rio e São Paulo a Belo Horizonte. As linhas poderiam ter rótulos indicando as distâncias entre as cidades.
Algoritmos em Grafos
Diversos algoritmos são utilizados para resolver problemas em grafos. A escolha do algoritmo depende do problema específico a ser resolvido. Alguns dos algoritmos mais comuns incluem:
- Busca em Largura (Breadth-First Search – BFS): Explora o grafo nível por nível, encontrando o caminho mais curto entre dois vértices.
- Busca em Profundidade (Depth-First Search – DFS): Explora o grafo seguindo um ramo até o final antes de voltar e explorar outros ramos.
- Algoritmo de Dijkstra: Encontra o caminho mais curto entre dois vértices em um grafo ponderado.

