O Plano Cartesiano e a Distância entre Dois Pontos: Definicao De Plano Cartesiano Distancia Entre Dois Pontos 5 Exemplos
Definicao De Plano Cartesiano Distancia Entre Dois Pontos 5 Exemplos – Este artigo explora o conceito fundamental do plano cartesiano, sua aplicação na determinação da distância entre dois pontos, e suas implicações práticas em diversas áreas. Começaremos com uma introdução ao sistema de coordenadas cartesianas, seguindo para a derivação e aplicação da fórmula da distância, ilustrados com exemplos práticos e exercícios para fixação do conhecimento.
Introdução ao Plano Cartesiano
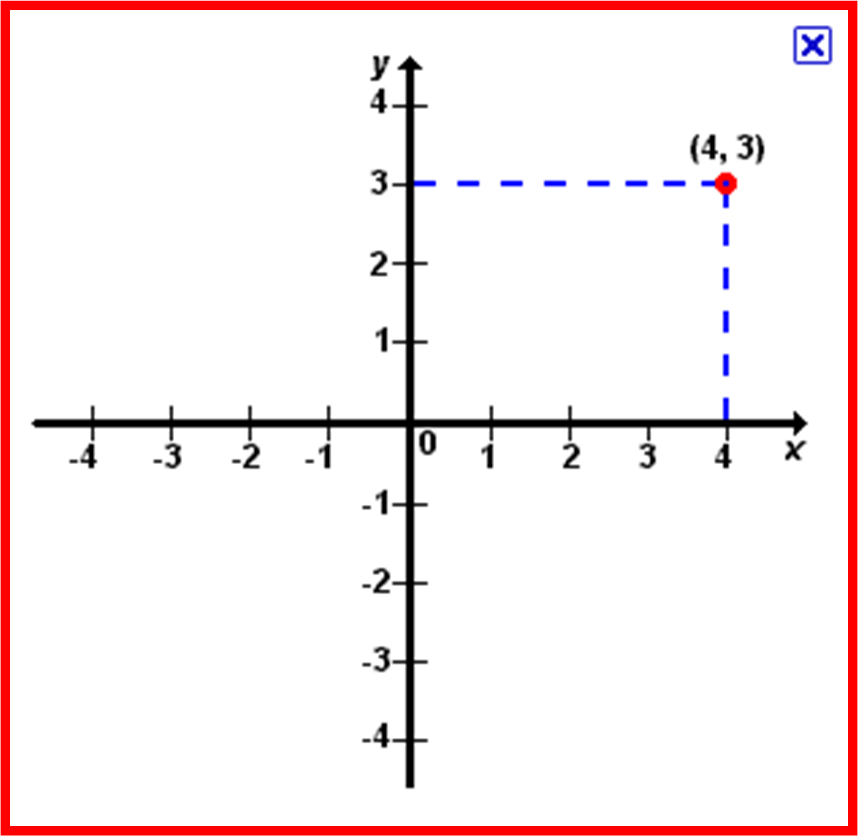
O plano cartesiano, também conhecido como sistema de coordenadas cartesianas, é uma ferramenta essencial em matemática e em diversas áreas científicas e tecnológicas. Sua estrutura básica consiste em dois eixos perpendiculares: o eixo x (horizontal) e o eixo y (vertical). O ponto onde os eixos se cruzam é chamado de origem (0, 0). Cada ponto no plano é unicamente identificado por um par ordenado de coordenadas (x, y), onde x representa a distância horizontal em relação à origem e y representa a distância vertical.
A importância do plano cartesiano reside na sua capacidade de representar graficamente relações matemáticas, permitindo uma visualização intuitiva de dados e equações.
Distância entre Dois Pontos
A distância entre dois pontos (x₁, y₁) e (x₂, y₂) no plano cartesiano é calculada utilizando o Teorema de Pitágoras. Imagine um triângulo retângulo com os dois pontos como vértices e a distância entre eles como a hipotenusa. Os catetos são as diferenças entre as coordenadas x e y dos dois pontos. A fórmula resultante é:
d = √[(x₂
- x₁)² + (y₂
- y₁)²]
Esta fórmula é aplicável em qualquer quadrante do plano cartesiano, garantindo a obtenção de uma distância sempre positiva, representando a distância euclidiana entre os dois pontos. A consistência da fórmula em diferentes quadrantes é garantida pelo uso do quadrado das diferenças das coordenadas, eliminando a influência do sinal.
Exemplos de Cálculo de Distância
Os exemplos a seguir demonstram o cálculo da distância entre pares de pontos, com crescente complexidade, facilitando a compreensão da aplicação da fórmula.
| Ponto A | Ponto B | Cálculo Detalhado | Distância |
|---|---|---|---|
| (1, 1) | (4, 5) | √[(4-1)² + (5-1)²] = √(3² + 4²) = √25 = 5 | 5 |
| (-2, 3) | (1, 0) | √[(1 – (-2))² + (0 – 3)²] = √(3² + (-3)²) = √18 ≈ 4.24 | ≈ 4.24 |
| (0, 0) | (5, -12) | √[(5 – 0)² + (-12 – 0)²] = √(25 + 144) = √169 = 13 | 13 |
| (-3, -4) | (2, 1) | √[(2 – (-3))² + (1 – (-4))²] = √(5² + 5²) = √50 ≈ 7.07 | ≈ 7.07 |
| (2.5, -1.5) | (-1, 3) | √[(-1 – 2.5)² + (3 – (-1.5))²] = √((-3.5)² + (4.5)²) = √32.5 ≈ 5.70 | ≈ 5.70 |
Aplicações da Distância entre Pontos, Definicao De Plano Cartesiano Distancia Entre Dois Pontos 5 Exemplos
O cálculo da distância entre pontos tem aplicações vastas. Na geometria analítica, é fundamental para determinar comprimentos de segmentos, perímetros e áreas de figuras geométricas. Em física, é usado para calcular deslocamentos e velocidades. Na engenharia, é aplicado em projetos de infraestrutura, como o cálculo da distância entre pontos de referência em um mapa para planejamento de rotas ou cálculo de distâncias em sistemas de navegação.
Um exemplo prático seria calcular a distância entre dois pontos de uma cidade em um mapa para determinar a rota mais curta entre eles usando um sistema de coordenadas.
Exercícios de Fixação
Resolver exercícios é crucial para consolidar o aprendizado. Os exercícios abaixo apresentam diferentes níveis de complexidade, permitindo a prática e a verificação do entendimento.
- Calcule a distância entre os pontos (2, 5) e (7, 11). Solução: √[(7-2)² + (11-5)²] = √(25 + 36) = √61 ≈ 7.81
- Determine a distância entre (-3, -2) e (4, 6). Solução: √[(4-(-3))² + (6-(-2))²] = √(49 + 64) = √113 ≈ 10.63
- Calcule a distância entre (1.5, -2.8) e (-0.5, 1.2). Solução: √[(-0.5 – 1.5)² + (1.2 – (-2.8))²] = √(4 + 16) = √20 ≈ 4.47
Representação Gráfica
A representação gráfica de dois pontos e da distância entre eles no plano cartesiano oferece uma visualização clara do conceito. Para isso, plotamos os dois pontos no plano cartesiano, utilizando uma escala apropriada para os eixos x e y. Em seguida, traçamos um segmento de reta conectando os dois pontos. A distância calculada é representada pelo comprimento deste segmento.
A rotulagem clara dos eixos, com indicação da escala utilizada, e a indicação da distância calculada sobre o segmento de reta, contribuem para uma representação precisa e compreensível. A visualização gráfica facilita a compreensão da relação entre os pontos e a distância calculada, tornando o conceito mais intuitivo.
Dominar o cálculo da distância entre dois pontos no plano cartesiano abre portas para um universo de aplicações práticas. De problemas geométricos a simulações complexas em física e engenharia, a capacidade de determinar com precisão a distância entre pontos é crucial. Através dos exemplos e explicações detalhadas apresentados, esperamos ter proporcionado uma compreensão sólida e intuitiva deste conceito fundamental.
Lembre-se: a prática leva à perfeição! Experimente resolver os exercícios propostos e explore as aplicações do que aprendeu. A geometria analítica, aparentemente abstrata, revela-se uma ferramenta poderosa e versátil, aplicável em diversos contextos da nossa realidade. Desvende os seus mistérios e aproveite o poder do plano cartesiano!

