Exemplo De Calculos De Fraçoes Com Denominadores Diferentes E Iguais – Exemplo De Cálculos De Frações Com Denominadores Diferentes E Iguais: Prepare-se para mergulhar no fascinante mundo das frações! Vamos explorar como somar, subtrair, multiplicar e dividir frações, tanto com denominadores iguais quanto diferentes. Desvendaremos os segredos do mínimo múltiplo comum (MMC) e como ele simplifica nossos cálculos, além de ver aplicações práticas dessas operações no dia a dia.
Dominar as frações é fundamental para diversas áreas, desde a matemática básica até aplicações mais complexas em física, engenharia e outras ciências. Neste guia, abordaremos cada operação passo a passo, com exemplos claros e objetivos, para que você se sinta confiante ao lidar com frações de qualquer tipo.
Frações: Um Mundo de Partes: Exemplo De Calculos De Fraçoes Com Denominadores Diferentes E Iguais

O universo das frações é fundamental para a compreensão de diversos conceitos matemáticos e sua aplicação prática no cotidiano. Desde a divisão de uma pizza entre amigos até cálculos mais complexos em engenharia, as frações permeiam nosso dia a dia. Este artigo explorará os fundamentos das operações com frações, focando nas diferenças entre frações com denominadores iguais e diferentes, e apresentando exemplos práticos para facilitar a compreensão.
Frações com Denominadores Iguais e Diferentes
A diferença crucial entre frações com denominadores iguais e diferentes reside na facilidade de sua manipulação. Frações com denominadores iguais podem ser somadas e subtraídas diretamente, somando ou subtraindo os numeradores e mantendo o denominador comum. Já as frações com denominadores diferentes exigem um passo adicional: a busca pelo mínimo múltiplo comum (MMC) entre os denominadores, para que possamos encontrar um denominador comum e, assim, realizar a operação.
O mínimo múltiplo comum (MMC) é o menor múltiplo comum a dois ou mais números. Ele desempenha um papel crucial na adição e subtração de frações com denominadores diferentes, permitindo que as frações sejam expressas com um denominador comum, facilitando a operação. Encontrar o MMC é essencial para garantir a precisão dos cálculos. A simplificação de frações, por sua vez, é importante para obter uma representação mais concisa e eficiente do resultado, reduzindo a fração aos seus termos mais baixos.
Adição e Subtração de Frações com Denominadores Iguais, Exemplo De Calculos De Fraçoes Com Denominadores Diferentes E Iguais
Operar com frações que possuem o mesmo denominador é intuitivo. Basta somar ou subtrair os numeradores, mantendo o denominador inalterado. A simplificação do resultado é um passo essencial para obter a forma mais simples da fração.
Exemplo de adição: 1/5 + 2/5 + 3/5 = (1+2+3)/5 = 6/5 = 1 e 1/5
Exemplo de subtração: 7/8 – 3/8 = (7-3)/8 = 4/8 = 1/2
A tabela a seguir ilustra os passos para resolver um problema envolvendo adição e subtração de frações com denominadores iguais:
| Passo | Operação | Descrição | Resultado |
|---|---|---|---|
| 1 | (5/9 + 2/9) – 1/9 | Adição e subtração de frações com denominador comum (9) | 6/9 |
| 2 | Simplificação | Divisão do numerador e denominador pelo seu máximo divisor comum (MDC), que é 3 | 2/3 |
Adição e Subtração de Frações com Denominadores Diferentes
Para somar ou subtrair frações com denominadores diferentes, é necessário encontrar o mínimo múltiplo comum (MMC) entre os denominadores. Este MMC se torna o novo denominador comum. Em seguida, ajusta-se cada fração, multiplicando o numerador e o denominador pelo fator necessário para obter o novo denominador comum. Só então, é possível somar ou subtrair os numeradores.
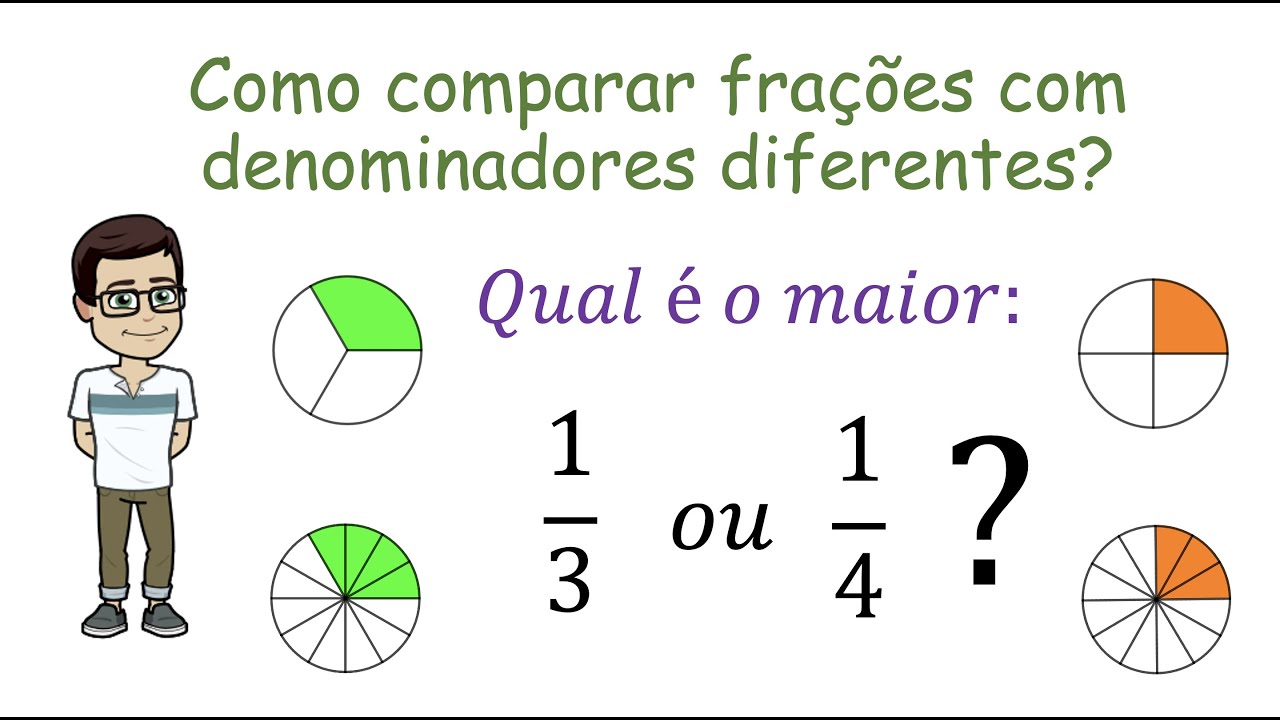
Considere a adição de 1/2 + 1/3. O MMC de 2 e 3 é 6. Então, 1/2 se torna 3/6 e 1/3 se torna 2/6. Somando, temos 3/6 + 2/6 = 5/6.
Um problema de subtração, como 5/6 – 1/4, pode ser resolvido com o MMC (12): 10/12 – 3/12 = 7/12. Sem o MMC, a operação seria consideravelmente mais complexa e trabalhosa.
Exemplo da adição de três frações com denominadores diferentes, utilizando o MMC e simplificando a resposta final:
– /2 + 2/3 + 1/6 = (3 + 4 + 1)/6 = 8/6 = 4/3 = 1 e 1/3
Multiplicação e Divisão de Frações

A multiplicação de frações é direta: multiplicam-se os numeradores entre si e os denominadores entre si. A simplificação do resultado final é aconselhada.
Exemplo: (2/3)
– (3/4) = (2*3)/(3*4) = 6/12 = 1/2
A divisão de frações envolve inverter a segunda fração e, em seguida, multiplicar as duas frações. Isto é, a/b ÷ c/d = a/b
– d/c.
Exemplo que envolve multiplicação e divisão de frações com denominadores diferentes:
- Calcular (2/5) ÷ (1/2)
– (3/4) - Inverter a segunda fração: (2/5)
– (2/1)
– (3/4) - Multiplicar os numeradores e os denominadores: (2*2*3)/(5*1*4) = 12/20
- Simplificar a fração: 3/5
Problemas com Frações no Cotidiano
As frações estão presentes em diversas situações cotidianas, facilitando a representação e resolução de problemas de divisão e proporção.
Exemplo de adição de frações com denominadores diferentes: Dividir uma pizza entre amigos. Se um amigo come 1/4 da pizza, outro 1/3 e um terceiro 1/6, a fração total consumida é 1/4 + 1/3 + 1/6 = (3 + 4 + 2)/12 = 9/12 = 3/4 da pizza.
Exemplo de subtração de frações com denominadores iguais: Um padeiro tinha 5/8 kg de farinha e usou 2/8 kg para fazer um pão. Restaram 5/8 – 2/8 = 3/8 kg de farinha.
Exemplo de multiplicação de frações: Um pintor precisa pintar 2/3 de uma parede. Se ele já pintou 1/2 da parte que precisa pintar, a fração da parede inteira que ele já pintou é (1/2)
– (2/3) = 1/3. A imagem representaria uma parede dividida em três partes iguais, com uma dessas partes pintada. A parte pintada representa 1/3 da parede inteira, que é o resultado da multiplicação das frações.
A imagem mental desta situação mostraria uma representação clara desta fração.

